De afsluitende vraag van Jan Aart in het wedstrijdverslag van LSG 3 tegen Philidor 2 hoop ik deels met het volgende verhaal te beantwoorden.
In “The Hitchhiker’s Guide to the Galaxy “van Douglas Adams, is het getal 42 het “Antwoord op de Ultieme Vraag van het Leven, het Universum en Alles”. Maar hij zei niet wat de vraag was! (Uiteraard is dit alles niet heel serieus bedoeld.)
De wiskundige John Baez geeft een goede kandidaat voor deze vraag. Zie daarvoor de volgende link. https://math.ucr.edu/home/baez/42.html Omdat het zo mooi is het volgende plaatje uit dit artikel.

Vanuit de natuurkunde zou de vraag kunnen zijn: “Uit hoeveel deeltjes bestaat een stiktofmolekuul?”
De aardatmosfeer bestaat voor het grootste deel uit stikstof. Een stikstofmolecuul bestaat uit 2 stikstofatomen. In het Bohr-model heeft een stikstofatoom een centrale kern, bestaande uit zeven protonen en zeven neutronen, omringd door zeven elektronen. Een stikstofmolecuul is dus opgebouwd uit 42 deeltjes!
Welke vraag zou voor schakers de Ultieme Vraag zijn?
In de begintijd van het schaken was er een stuk dat firzan heette. Dit was een loper die elke zet maar 1 veld kon verschuiven. Of ook wel een damschijf vermomd als loper. Het is verrassend genoeg niet de voorloper van de loper, maar van de koningin. De geschiedenis van de schaakstukken wordt onder meer in de inleiding van de serie “Wij Presenteren” van Hans Böhm en Yochanan Afek beschreven.
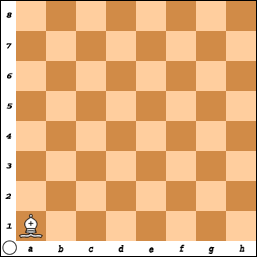
Op a1 staat een firzan.
We kunnen ons afvragen wat de afstand voor dit stuk tot bijvoorbeeld f2 is. En vervolgens de vraag stellen hoeveel verschillende kortste routes er van a1 naar dit veld voor dit stuk zijn. Het is duidelijk dat er maar 1 kortste route is van a1 naar ieder veld op de hoofddiagonaal. Om het aantal kortste routes van a1 naar f2 te vinden kan je opmerken dat het voorlaatste veld in zo’n kortste route e1 of e3 is. De aantallen kortste routes van e1 en e3 bij elkaar opgeteld geven dus het aantal kortste routes naar f2: 2+3=5.
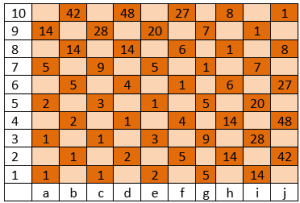
In de tabel staan de aantallen kortste routes voor de firzan vanaf a1 tot elk bruin veld.
De getallendriehoek op en onder de hoofddiagonaal staat in de wiskunde bekend als “De driehoek van Catalan.” Zie https://mathworld.wolfram.com/CatalansTriangle.html
De vraag van Jan Aart welk van de drie getallen 12, 28 en 42 het belangrijkste is kan ik niet beantwoorden, maar toevallig zien we op bovenstaand bord de getallen 28, 42 en 48(=4×12) naast elkaar staan!
Het getal 42 vinden we niet op het schaakbord, maar wel op het dambord. De Ultieme Schaakvraag blijkt een Damvraag te zijn!
“Op hoeveel verschillende manieren kan een damschijf op een verder leeg dambord in zo weinig mogelijk zetten van veld 46 (=a1) naar veld 1 (=b10) gaan?”
Als we de velden met even aantallen kortste routes geel kleuren en die met oneven blauw ontstaat het volgende patroon.

